はじめに
前回の記事で、ディープラーニングを図と数式で説明しました。
そして、記事の最後にパラメータの計算方法について、説明できていないこともお話ししました。
そこで今回は、ディープラーニングのモデルについて、パラメータを計算する方法を説明します。
ただし、こちらを学ぶためには「数学の微分とベクトル解析」、「コンピュータで最小値を求める時の考え方」が必要となります。
もし、徹底的に理解したい方は、今後のためにもこれらを学ぶことをオススメします。
また、考え方の雰囲気を知りたい方は、細かい計算式は飛ばして、考え方の流れを掴んでもらえればと思います。
自分自身で、この内容を理解してプログラムを書く必要はないので、この情報は「より理解を深めたい人」向けの補足になります。
画像判定ディープラーニングの復習
今回も、前回の記事で用いた画像判定ディープラーニングで説明を進めます。
まずは、そのまとめを整理してきましょう。
全体像
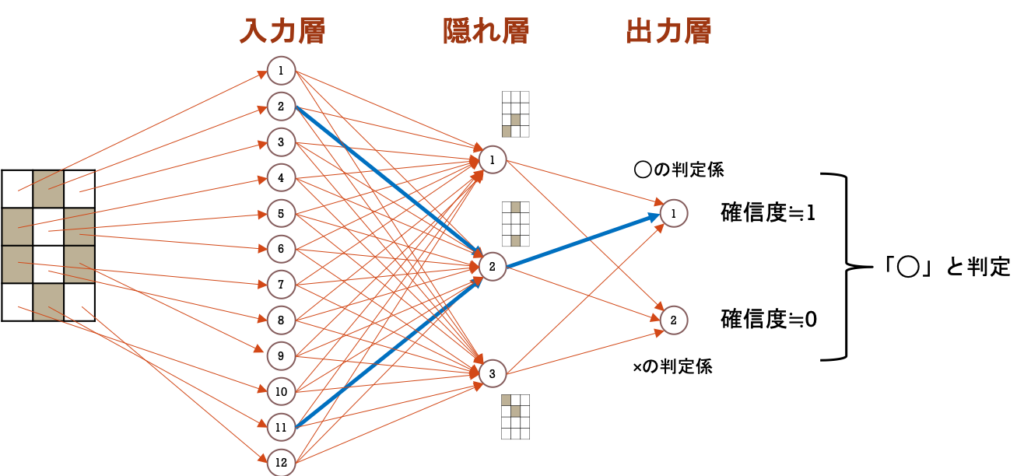
記号の定義

第2層:隠れ層(Hidden Layer)
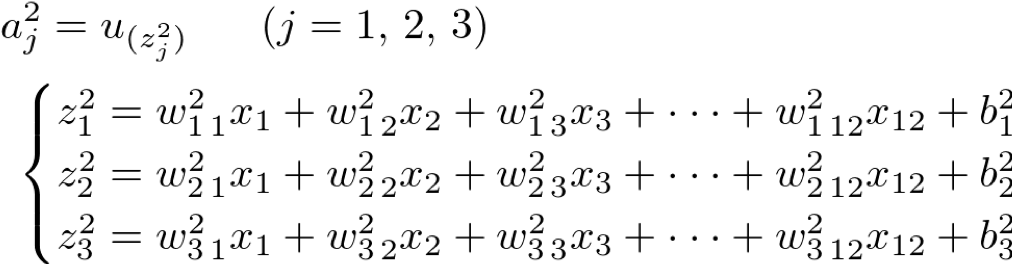
第3層:出力層(Output Layer)
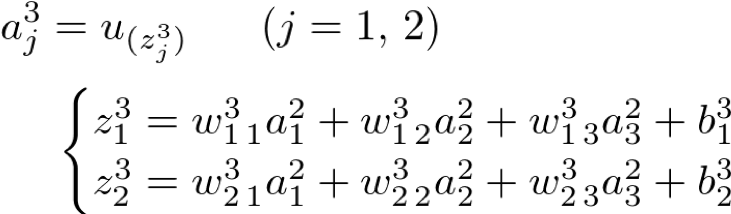
(補足)
コスト関数の設定
パラメータを計算するためにはコスト関数を設定する必要があります。
コスト関数は、モデルと実際のデータの「誤差の総量」を表しています。
つまり、これが小さくなるパラメータを計算で求められれば、実際のデータに合ったモデルとなります。
※パラメータを計算する考え方を知りたい方は、次の記事をご参照ください。
コスト関数とは、「モデルで計算した判定結果」と「実際の正解」の差となります。
つまり、あるk番目のデータを利用して、○と×の判定(確信度)の結果がaで、正解がtだったとします。
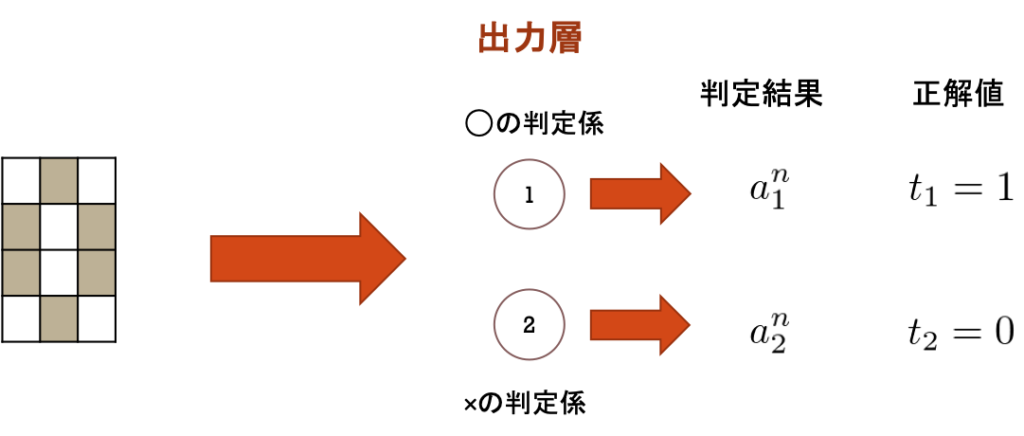
この場合の誤差 c は、次のように表せます。
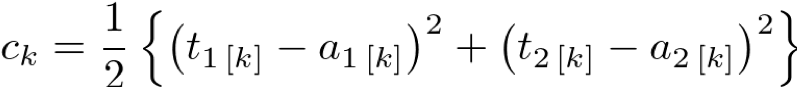
ただし、これはk番目のデータ1つの誤差です。
データがもっとたくさん(データがn個)ある場合は、この細かい誤差を全て足す必要があります。
そのため、最終的なコスト関数は次のようになります。

コスト関数から最適なパラメータを計算する「勾配降下法」
コスト関数が設定できたので、これを元にパラメータを求めます。
まず、コスト関数が最小になるための条件として、お馴染みの微分した結果が”0″となる数式を設定します。
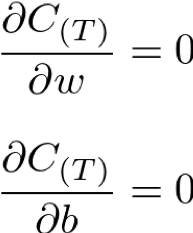
しかし、またまた問題があります。
主な点では・・・
1つ目:コスト関数 C(具体的には人工ニューロンに設定した関数)の詳細が未定であること。
2つ目:毎回手作業で微分の計算をしては手間がかかりすぎること
そこで、コスト関数の詳細にかからず、コンピュータに計算させる方法として、勾配降下法が作られました。
コンピュータで最小値を求める方法
コンピュータで関数の最小値を求める時の代表的な考え方に、現在の値より小さい値を持つようにパラメータを更新し続け、最終的に最小点へ到達させる方法があります。
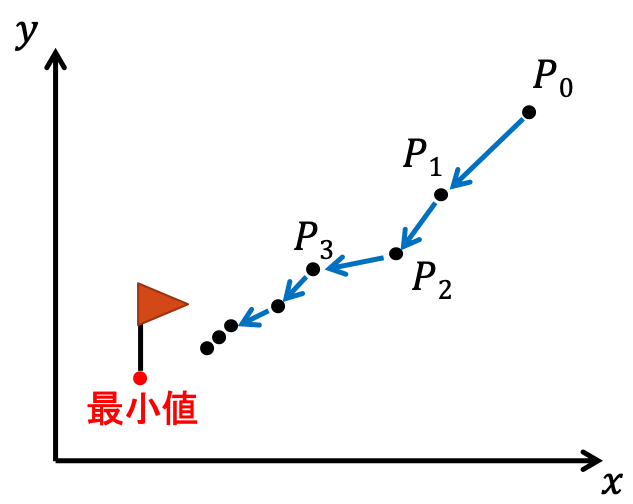
この方法で重要なのが、現在の値より小さい値を持つようにパラメータを更新するルールです。
今回は、このルールの中から「勾配降下法」と呼ばれるモノを紹介します。
勾配降下法の導出
説明を簡単にするために、パラメータが2つの場合の関数 z = f(x, y) について考えることにします。
この関数について、x → x+Δx、y → y+Δy とごく僅かだけ値をズラすとします。
そうすると当然 zも少しズレるので、そのずれ幅Δzを考えます。

ここで、微分法の定義を確認してみます。
はじめに、1変数の場合の微分法の定義は
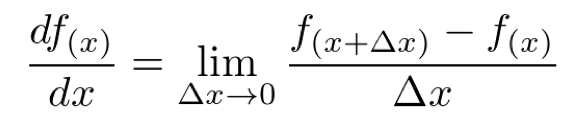
ここで、Δx が非常に小さい時、微分法の定義は次のように近似できます。
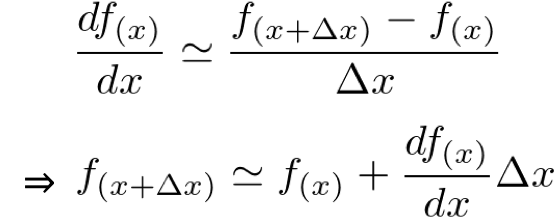
これを、2変数の場合に拡張すると次のような式になります。
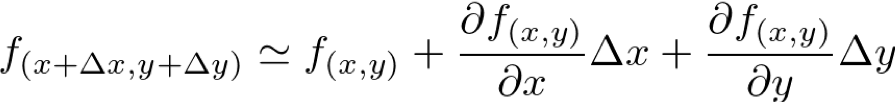
ここで、左辺の項がeq.(1)に含まれているので、代入します。

次に、eq.(2)の右辺がベクトルの内積の形に似ているので、以下のように表します。

ここで、ベクトルの内積の定義が
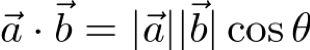
cosθ=-1〜1 なので、Δz が最小のなるのは以下の式を満たす時になります。
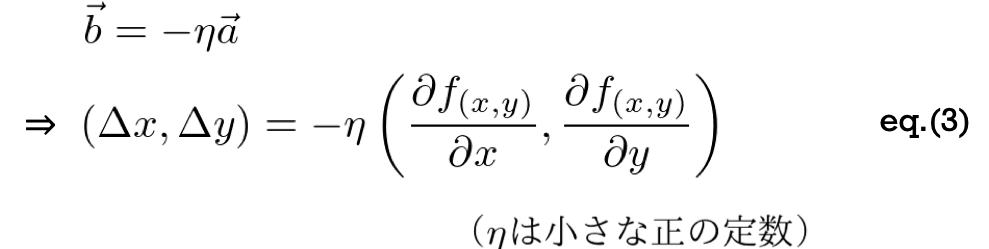
したがって、関数 z = f(x, y) のある点(x1, y1)から x と y を少しズラして、z1+Δz を最小にしたいならば、次のように(Δx, Δy)をズラせばよいことになります。
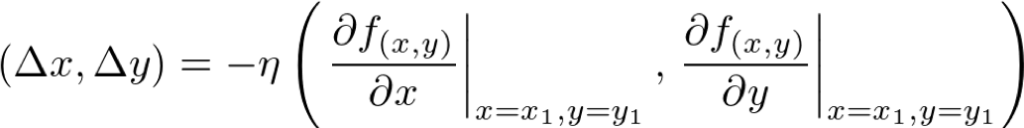
このルールに従って、x と y を繰り返しズラすことで、z を真の最小値までズラすことができます。
勾配降下法の解釈
勾配降下法の導出した式(eq.(3))をよく見ると、右辺の()内は関数 f(x, y) の勾配を表しています。
※勾配とはグラフの傾きのことです。

つまり、この f(x, y) のグラフを図のように単純化すると、z を最小値に向かうように点P→点Qにズラす様子は以下のように表すことができます。

これは、グラフの勾配に対して、真逆に進んでいる様子を示しています。
「勾配」という言葉に聞き馴染みがないとピンとこないかもしれませんが、簡単にいうと・・・
グラフを坂道に例えると、坂道の登り方向(≒ 勾配)と逆向き向かって移動する。
すなわち、坂道を下っているので、いつかは一番低い場所にたどり着けるはず!!
「勾配降下法」をディープラーニングに適用
勾配降下法によって、コンピュータが得意な「繰り返し計算」によって関数の最小値を求めることができます。
早速、勾配降下法にコスト関数を当てはめてみましょう!!

・・・あれ? 偏微分が消えてない!?
実は、コンピュータだけでコスト関数の最小値を求めるさせるためには、勾配降下法だけでは不十分なのです・・・
この問題は、本当にコンピュータだけで解かせるためには「誤差逆伝搬法」を導入する必要があります。






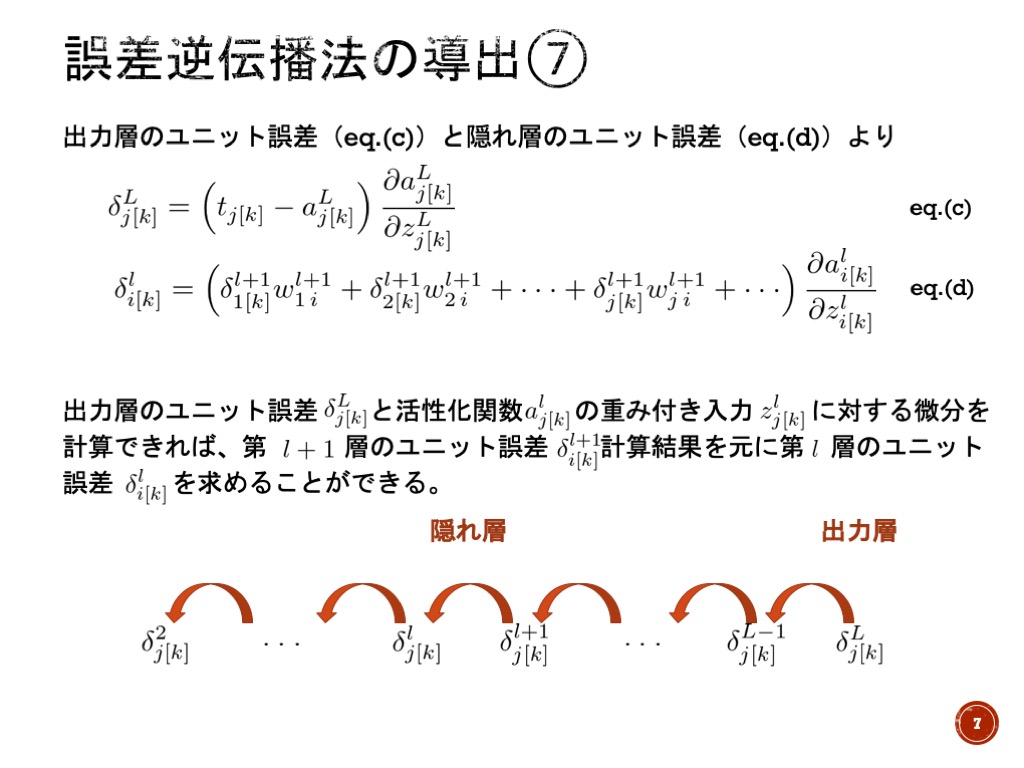

まとめ
ディープラーニングのモデルでパラメータを計算する方法をまとめると次のようになります。

このプロセスを繰り返すことで、最適なパラメータを求めることができます。
最後に
これで、ディープラーニングのモデルを原理から理解し、パラメータの決定方法まで学ぶことができました。
もしかしたら、途中でよく分からなくなってしまった方もいるかもしれません。
その場合は、落ち着いて一つ一つの式を丁寧に見返してみてください。
または、自分の手で式変形を丁寧に紙に書いてみると、繋がりが見えてくると思います。
難しいと思いますが、ぜひこの内容を自分の物にできるように、チャレンジしてみてください!






コメント