はじめに
2010年代に、AI、機械学習、ディープラーニング、という言葉は世界を変える新技術のように流行していました。
そして、広告では何かにつけて「AIを使った〇〇」や「AIで開発した〇〇」と、AIが万能であるように語られています。
でも、ちょっと待ってください・・・
そもそも、AIって何でしょう??
それに、AIと一緒に、機械学習やディープラーニングという言葉をよく聞くけど、一体何者でしょう??
今回は、これらの疑問に真正面から向き合ってみようと思います!!
この記事を読んでいただいた後に、みなさんの中で「AIってこういうモノだよね」と納得するコアを持っていただけると嬉しいです。
AIというモノを整理する
AIの定義とは?
最初に、AIという言葉を掘り下げていきます。
AIとは、「Artificial Intelligence」の頭文字を取った言葉です。
回りくどいですが、丁寧に整理すると次のようになります。

すなわち、AIを「人工知能」と和訳しますが、厳密な定義は存在しないのです・・・
AIと呼ばれているモノの正体
AIに厳密な定義が存在しないならば、「世間でAIと呼んでいるモノ」は何でしょうか?
それは、各時代の先端技術で、人間の知的活動を模倣・補佐できるモノをAIと呼んでいるのです。
実際、過去に2回のAIブームがあったと言われ、現在は3回目のブームになります。
第1次AIブーム(1960年代)
ルールとゴールが定義された環境で、最良の解を探索する仕組み
→ゲームや迷路の探索程度以上の成果を上げられず、ブームは終焉・・・
第2次AIブーム(1980年代)
知識をルールや辞書として人間が記述し、そのルールと辞書に基づいて処理を行う仕組み
→世の中のあらゆる事象をルール化できず(汎用性がない)、ブームは終焉・・・
第3次AIブーム(2010年代)
HW処理性能やビックデータ活用技術の向上を背景に、機械が自ら学ぶ仕組み(機械学習)を実現
第1、2次AIブームの失敗は、人間が世の中にある全ての知識/ルールをコンピュータに教える(プログラミングする)ことを目指したことにありました。
(そもそも、不可能ですよね・・・)
そのため、今回(第3次AIブーム)は、機械が自ら学ぶ仕組みを取り入れました。
これならば、人間がコンピュータに知識/ルールを教える作業が不要となります!
機械学習やディープラーニングとの関係は?
AI、機械学習、ディープラーニングを関係性は、次の図で表すことができます。
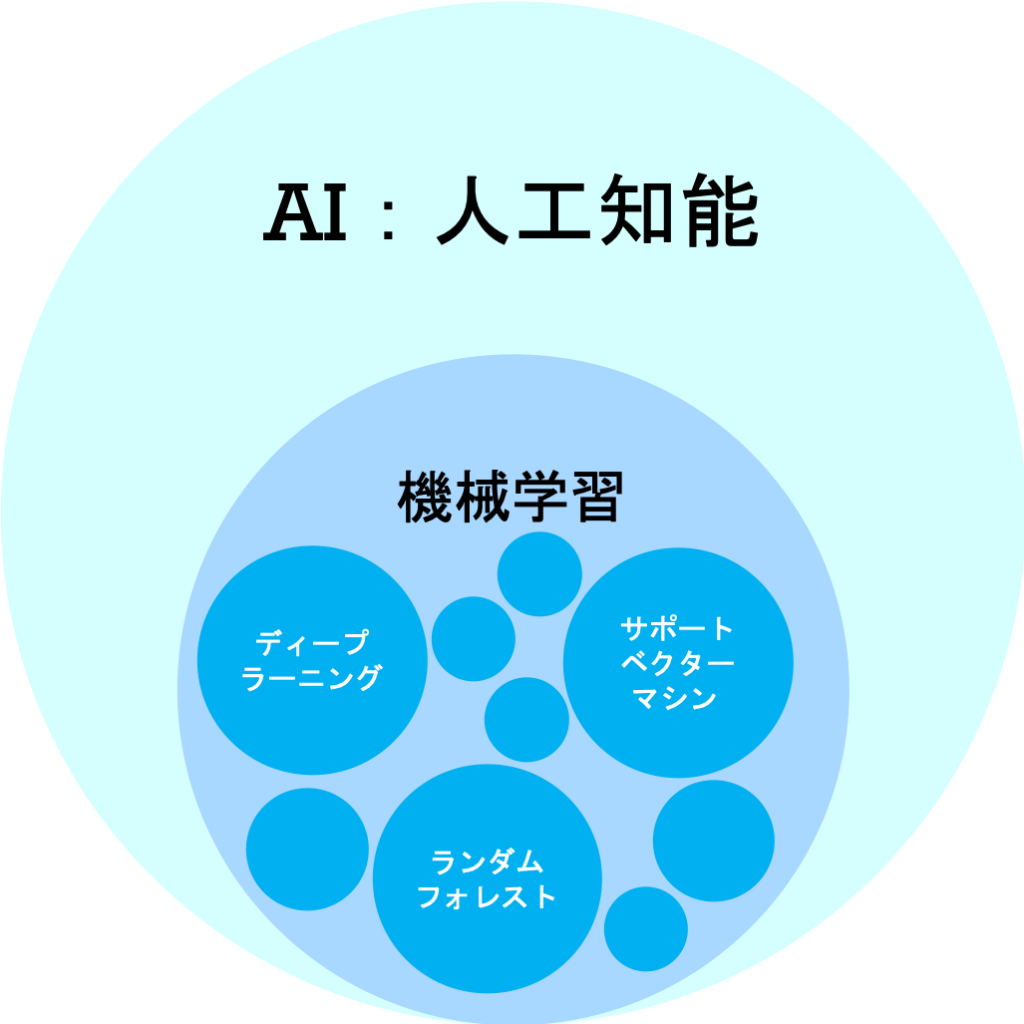
まず、AIと言う「人間の知的活動を模倣・補佐できるモノ」が大枠としてあります。
機械学習は、「AIを作るための技術の1つ」になります。
ディープラーニングは、「機械学習の具体的な方式の1つ」です。
機械学習の方式は他にもあり、日々開発/改良が進められています。
機械学習(機械が自ら学ぶ)とは?
自分の目の前にあるコンピューターに向かって、「自分で学んでね」と言っても・・・
もちろん、何も起こりません(笑)
機械学習も、所詮は人間が「プログラミングしたモノ」に過ぎないのです。
では、学習とはどのようなプログラムになるのでしょうか?
ここでは、機械学習の方式の1つである「単回帰モデル」を用いて説明します。
単回帰モデルで、機械学習のイメージを掴む
ある店舗で1日毎に「客数」と「売上」を集計しているとします。
これをグラフ上に描く(プロットする)と、右肩上がりの分布しているように見えました。

青い直線は、パラメータ(aとb)を決めると完成します。
では、このパラメータ(aとb)はどのように求めればよいでしょうか??
1つの答えが、「直線と各点(データ)のズレの合計が最小になれば良い!」になります。
言葉では難しく聞こえますが、イメージはとても単純です。
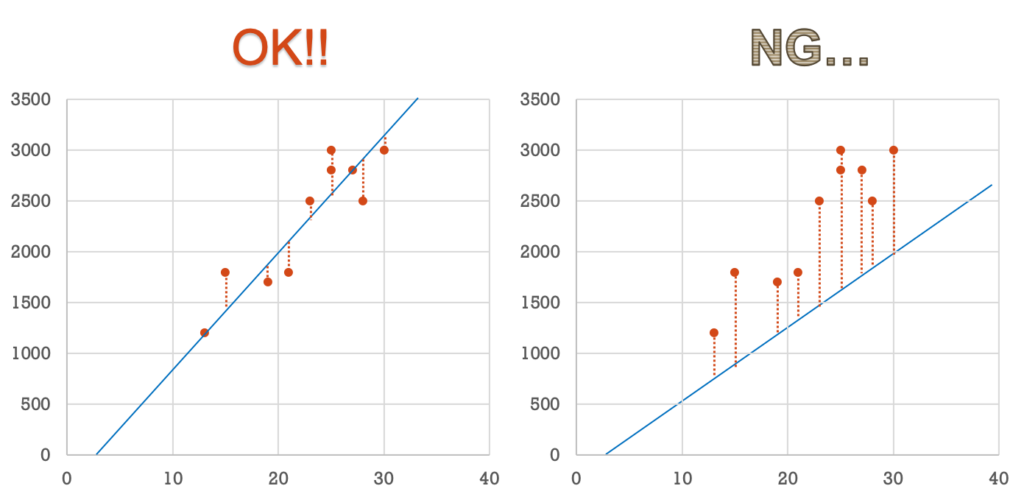
具体例を使って、単回帰モデルを計算する
青い直線(パラメータ:aとb)を求める方針を「ズレの合計が最小」に決めることにしました。
では、今回の例では、各点(データ)でのズレを計算してみます。
本来なら y=ax+b となっているので、y と ax+b は一致するハズです。
しかし、グラフを見て分かる通り、残念ながら一致はしていないため、「y – (ax+b)」だけズレています。
全ての点(データ)に対してこのズレを1つずつ計算します。
※最後に2乗しているのは、+とーが混在しないように工夫しています。

この一番右の列が、各点(データ)のズレとなります。
このズレを合計した物を「誤差関数」や「コスト関数」と呼びます。
※ここでの呼び名は「コスト関数」とします。

数字や数式がたくさん出てきましたので、一旦整理すると・・・
・目的は「ズレの合計が最小」となる青い直線(パラメータ:a, b)を求める!
・青い直線と各点(データ)とのズレを計算した
・全てのズレを合計して、それをコスト関数と呼ぶことにした。
お気づきだと思いますが、これまでの作業で「ズレの合計が最小」という漠然とした目的を、数式をつかった「コスト関数が最小」に具体化することができました。
あとは、コスト関数が最小となるパラメータ(a, b)を求めるだけです!!
ただ、この計算には高校数学で習う微分の発展版である「偏微分」という知識が必要になります・・・
そのため、数式と計算結果のみの紹介とさせていただきます。
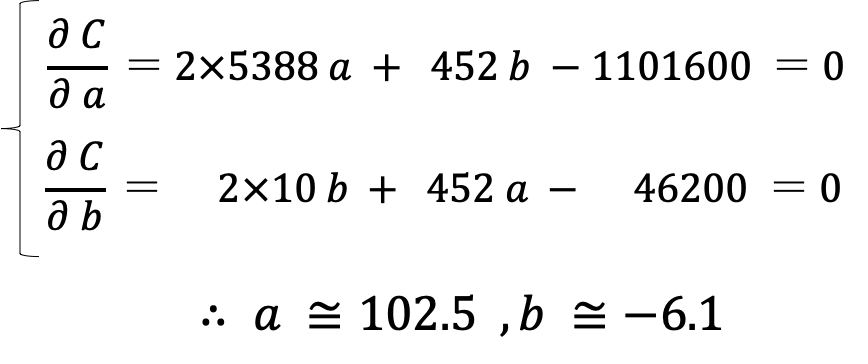
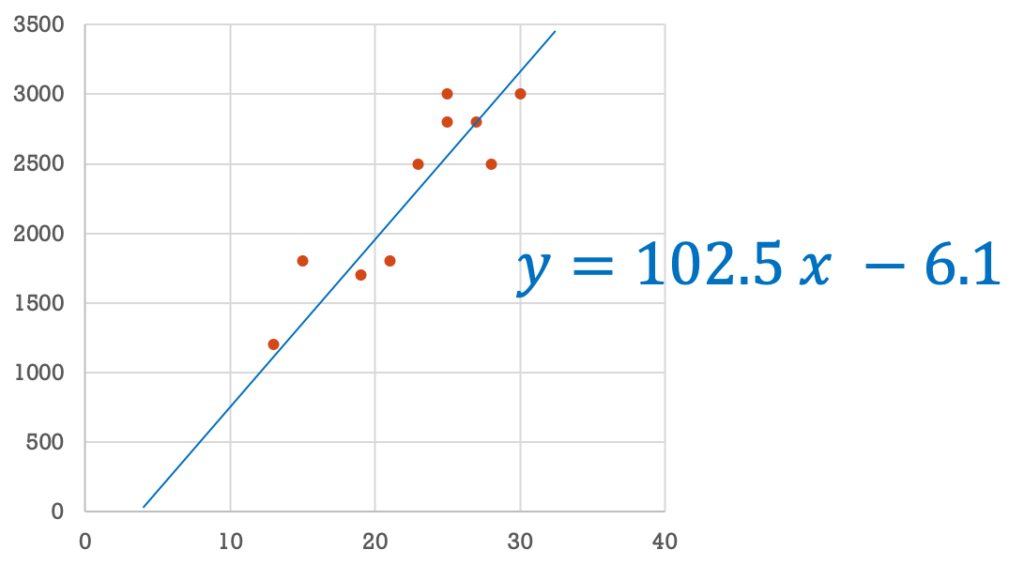
このように、「ズレの合計が最小」=「コスト関数が最小」という目的に従って、データからパラメータ(a, b)を求める作業を「パラメータ探索」や「パラメータフィッティング」と呼びます。
機械学習のまとめ
具体例から、機械学習でKeyとなる4つの言葉を用いて纏めます。
モデル
モデルとは、求めたい状況を数式で表したものになります。
機械学習では、状況にあったモデルを適切に選ぶことが大切となります。
各モデルがどのような特性を持っているかは、選定時に理解しておくようにしましょう。
具体例では、求めたい状況が直線の関係になっていました。
そこで「y = ax + b」という数式(モデル)を使用しました。
この数式は、「単回帰モデル」と呼ばれています。
モデルには、単回帰モデルのような単純な数式で表せるものから、(見たこともないような)高等数学で表すもので多種多様に存在しています。
パラメータ
モデルを選定した段階では未決定で、データを使って適切な値が計算されるモノになります。
モデルを選定することで求めたい状況の大枠を決めることができます。
そして、パラメータを計算することで、求めたい状況を具体化させます。
コスト関数(誤差関数)
実際のデータとモデルのズレの合計を表した関数になります。
この関数が最小になるようなパラメータを計算するために用います。
学習(パラメータ探索/パラメータフィッティング)
実際のデータとコスト関数を利用してパラメータを求める作業となります。
コンピュータがデータを読み込んでパラメータを計算する様子を「学習している」と表現しています。
すなわち、機械学習とは「コンピュータが、データを用いてコスト関数を最小化するパラメータを計算する作業」と言い換えることができます。
また、この時に使うデータを「学習データ」と呼びます。
最後に
「AIの記事を読んでたのに、いつの間にか数学の勉強になってる・・・」とビックリした方も多いと思います。
実は、第3次AIブームのコア技術である機械学習は高度な数学によって支えられているのです!!!
・学習と呼ばれる、モデルのパラメータを求めるための解析学
・学習に使用する膨大なデータを扱うための統計学
・モデルそのものを構築するための高等数学(代数、幾何学、グラフ理論・・・)などなど
このことに目を背けていると、いつまで経っても機械学習はブラックボックスのままです。
今から全てを勉強することは困難ですが、必要になった時に調べる取っ掛かりを作ると良いと考えています。
引き続き、理解の手助けになるような情報を発信しているので、こちらもご覧ください!






コメント