はじめに
AIとディープラーニングは、よく混同して使われています。
こちらの記事でAIは「知的活動を模倣するモノ(概念)」、ディープラーニングは「AIを作るための技術である機械学習の方式の1つ」と紹介しました。
※詳しく知りたい方はご参照ください。
それでは、ディープラーニングとは具体的にはどのようなものでしょう?
ご存知の方は、ディープラーニングを調べると「ニューラルネットワーク」という言葉も出てきますね。
この2つの違いは一体何なのでしょうか?
今回は、ディープラーニングに真正面から向き合ってみようと思います!!
「ディープラーニング」は「ニューラルネットワーク」の中の1つ
見出しでネタバレをしましたが、「ディープラーニング」は「ニューラルネットワーク」の中の1つに過ぎません。
関係性を図で表すと次のようになります。
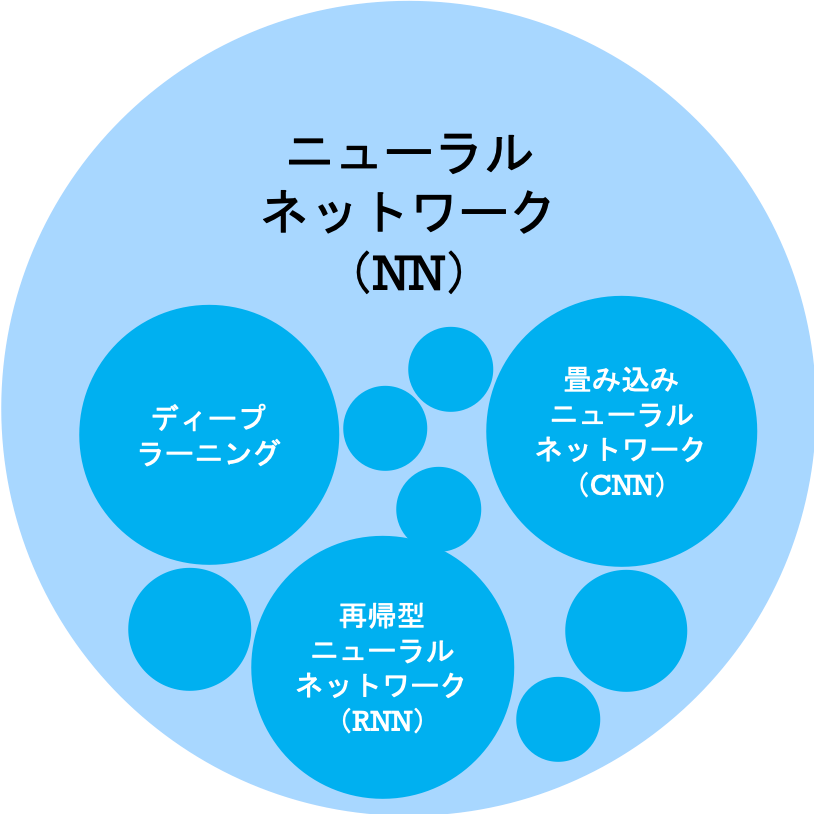
詳細は後述しますが、ニューラルネットワークではデータを層に区切って処理します。
データを第1層で処理して、第2層に引き渡す
→第2層はデータを受け取ったら処理して、第3層に引き渡す
→第3層はデータを受け取ったら処理して、第4層に引き渡す
→ ・・・
ディープラーニングとは、ニューラルネットワークの内、層が多い(深い)モノを示します。
厳密に「○層以上をディープラーニングと呼ぶ」のような定義はないので、慣用表現のような扱いになります。
また、ニューラルネットワークの中には他にも種類がありますが、今回は割愛させていただきます。
ディープラーニングの概要
ディープラーニングは、実際の生き物の脳の働きをマネすることで知性を再現しようとして生まれた方式です。
実際の生き物の脳では、複数のニューロンが情報をやり取りすることで知性が生まれています。
そこで、生き物のニューロンに働きと似せた人工ニューロンをプログラムで作り、人工ニューロンを結び付けてデータをやり取りさせることができれば「知性が再現できるのでは?」と考えました。
生き物の脳をプログラムで再現する
すこし強引ですが、生き物のニューロンにプログラミングで必要な情報を重ね合わせてみます。
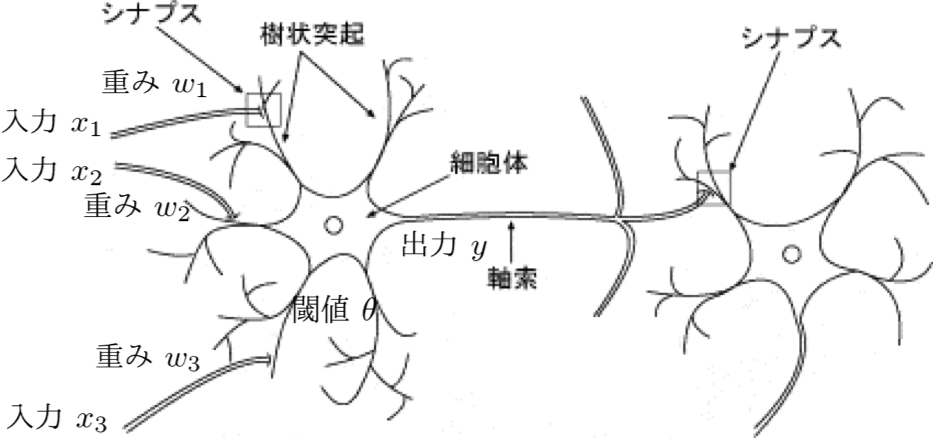
(2) 受信した入力信号が、ニューロンの固有値(閾値θ)を超えると発火する
(3) ニューロンが発火すると出力信号 y を発信する
※本来のニューロンが発する信号はあり/なしのみ
このような働きをする人工ニューロンを作ることができれば、ディープラーニングに必要なパーツを揃えることができます。
人工ニューロンを紹介
人工ニューロンに必要な3つの働きを数式で表すと次のようになります。

これは、重み付き和が閾値θを下回れば出力が “0” 、閾値θを上回れば出力が “1” ということを表しています。
しかし、このままでは「→」で繋がって左右の式が分離しています。
そこで、この2つの式で次のように纏めることにします。
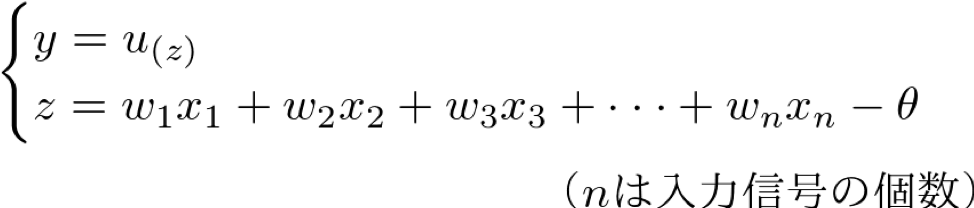
1つ目の式の右辺:u(z) は、人工ニューロンの性質をよく表し、計算が容易な関数にする必要があります。
この関数は、活性化関数と呼ばれています。
ここでは、数ある人工ニューロンに使われる活性化関数から、2つほど紹介します。
ステップ関数
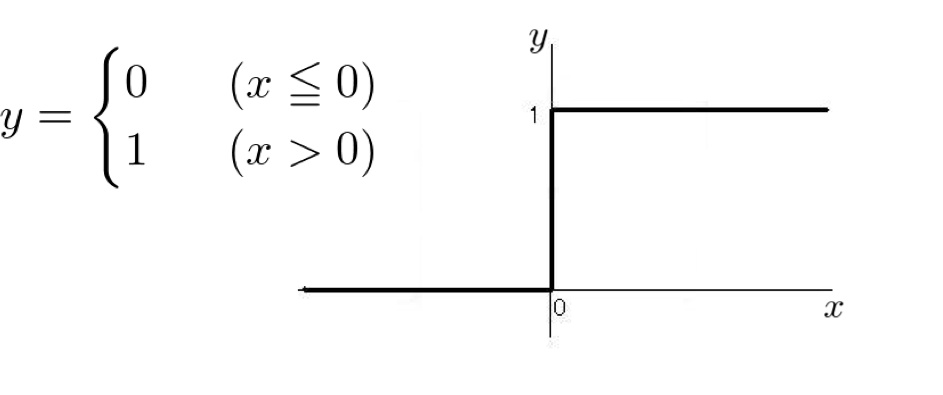
ステップ関数は、本来のニューロンの性質を最もよく表せているため、活性化関数の候補に考えられていた。
※ステップ関数を用いた人工ニューロンモデルは、パーセプトロンモデルと呼ばれている。
シグモイド関数

シグモイド関数はステップ関数で問題となった関数の連続性を保持している。
さらに、xが小さくなれば0に、xが大きくなれば1に近づくという、実際のニューロンに近い性質を持っている。
このような便利な性質があるため、活性化関数として利用されている。
※シグモイド関数を用いた人工ニューロンモデルは、シグモイドモデルと呼ばれている。
ディープラーニングの図解
人工ニューロンというパーツができました。
次はこれを組み合わせて情報をやり取りするネットワークを作ります。
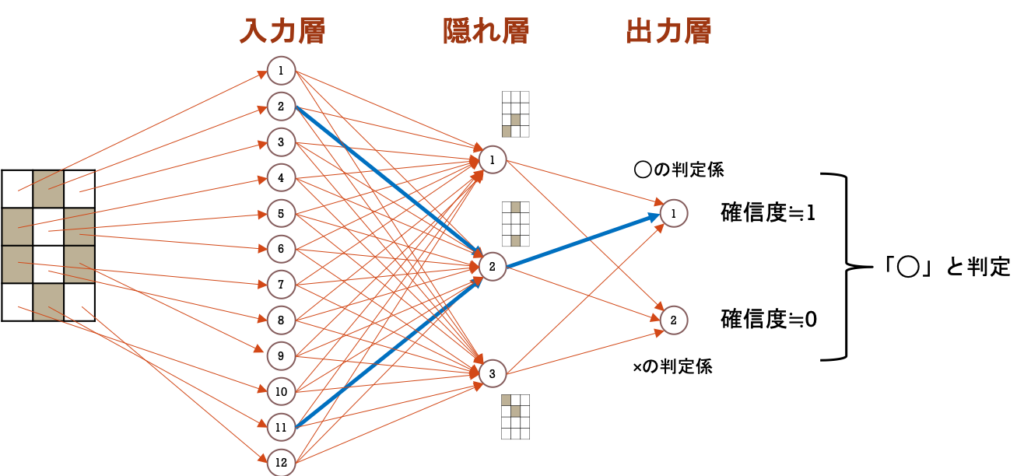
今回は、「○と×の画像データ」を判定するモデルを例に説明します。
そのために、人工ニューロンを入力層、隠れ層、出力層の3層に配置します。
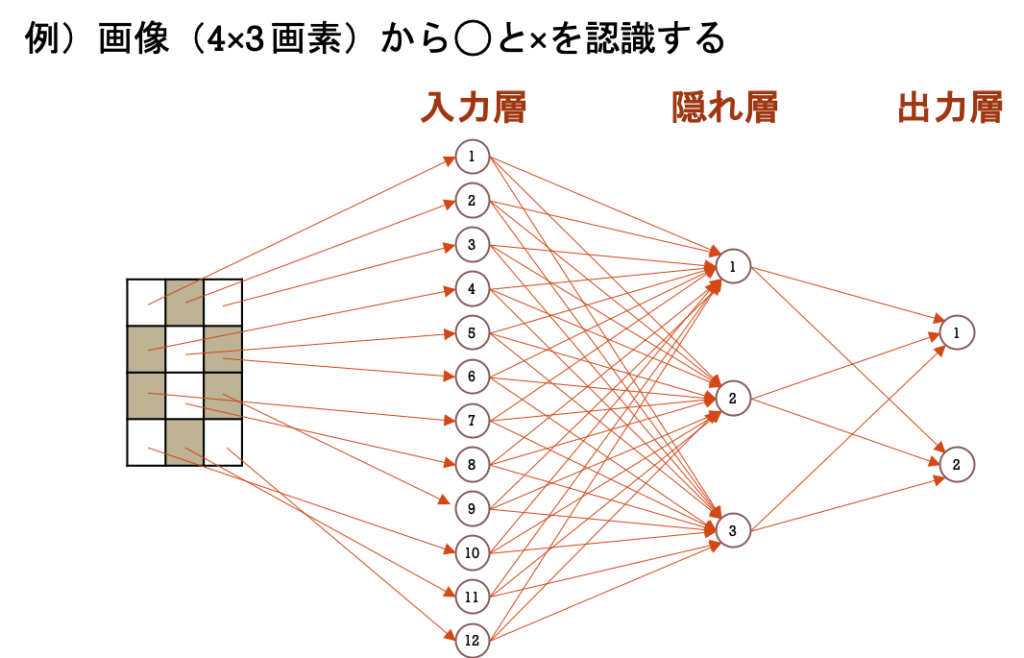
「入力層(Input Layer)」の役割
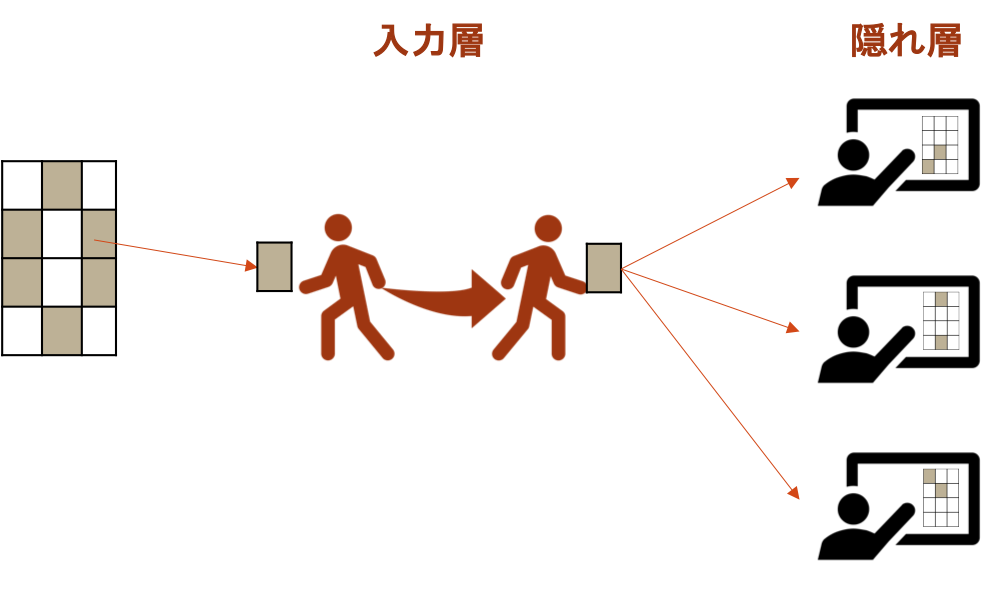
入力層は、画像データから取得した情報を一切加工することなく、隠れ層へ受け渡します。
すなわち、画像データから隠れ層へ情報を運ぶ運搬係となります。
「隠れ層(Hidden Layer)」の役割
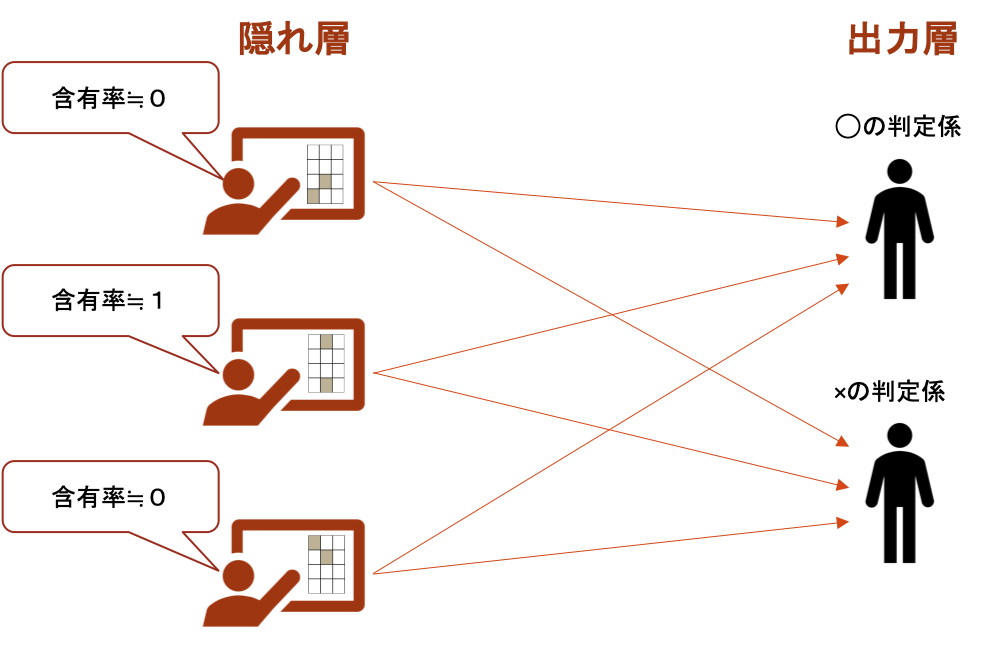
隠れ層は、入力層から運ばれてきた情報と各人工ニューロンが受け持つパターンを比較します。
そして、運ばれてきた情報に受持パターンが含まれている割合(含有率)を計算し、次の層へ受け渡します。
すなわち、画像データと受け持ちパターンとを比較する検知係となります。
「出力層(Output Layer)」の役割
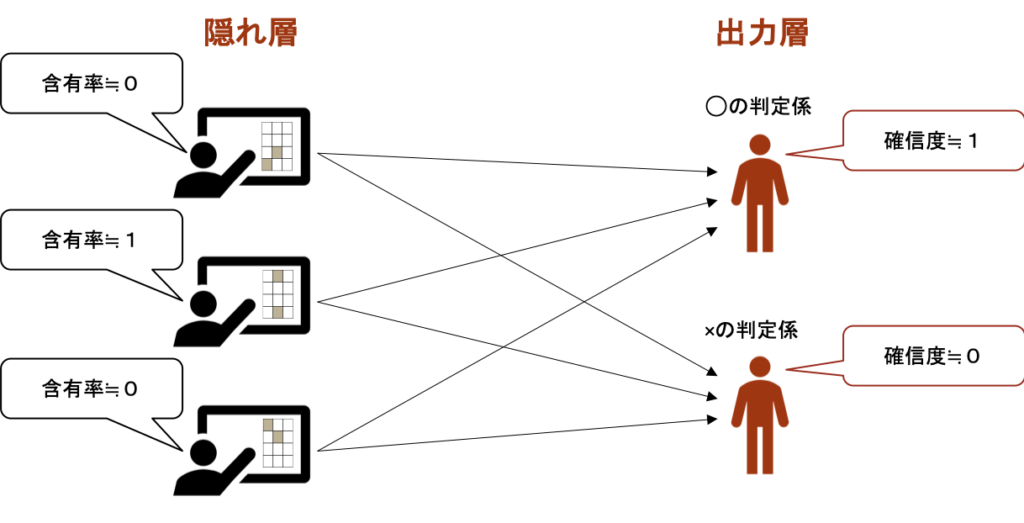
出力層は、隠れ層から受け渡された情報をもとに、各人工ニューロンが受け持つ識別パターンと合っているかを数値化します。
この数値化されたモノを確信度として扱います。
すなわち、画像データと識別パターンを比較する判定係となります。
パラメータの役割
ディープラーニングを構成する入力層、隠れ層、出力層が整理できました。
次に、(ディープラーニングに限らず)モデルの具体的な性質を決めるパラメータについて、役割をみていきます。
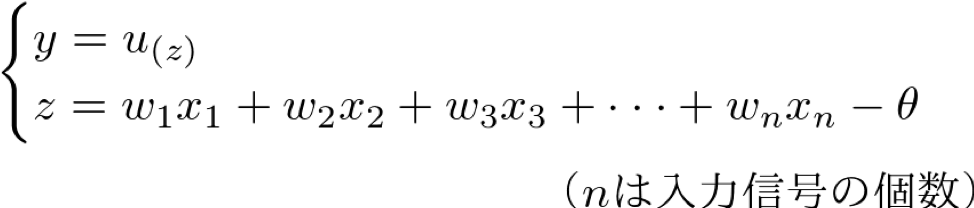
「重みw」の役割
各層に配置した人工ニューロンが発信する情報(値)は 0〜1 となります。
この情報をそのまま次の層に受け渡してしまっても良いのですが、1つ疑問が出てきます。
それは、「各人工ニューロンから受け取った情報を全て同じように扱って良いか(優劣はないか)」ということです。
たとえば、人の顔を判定する時、「顔の輪郭」や「目の形」に関する情報と「髪型」や「おでこの形」の情報は同じ扱い・・・ではないですよね。
この問題を解消するために、情報の重要度を数値化することにしました。
これが、重み w というパラメータになります。

「閾値(バイアス)θ」の役割
重み w は人工ニューロンが情報のやり取りをする時に使われるパラメータでした。
もう一つの考え方として、ニューロン自身が計算をする時に重要度を上げ下げすることにフォーカスします。
この時に、使うパラメータが閾値(バイアス)θです。
例えば、「目の形」を扱う人工ニューロンは、閾値θを小さくして重要度を上げます。
また、「髪型」を扱う人工ニューロンは、閾値θを大きくして重要度を下げます。
閾値をバイアスと呼ぶのは、ディープラーニングを人に見立てたとき、「閾値θは、データを処理する時の偏り」と捉えることができるためです。
ディープラーニングの全体像
・入力された情報を一切加工せず次の層へ受け渡す。
隠れ層
・重要度が付加された情報を受け取り、パターン検知処理を行う。
・処理結果は次の層に受け渡す。
出力層
・重要度が付加された情報を受け取り、判定処理を行う。
重要度
・パラメータ(重みwとバイアスθ)で表す。
ディープラーニングの数式化
これまでの説明をイメージした上で、ディープラーニングを数式で表します。
記号の定義

第2層:隠れ層(Hidden Layer)
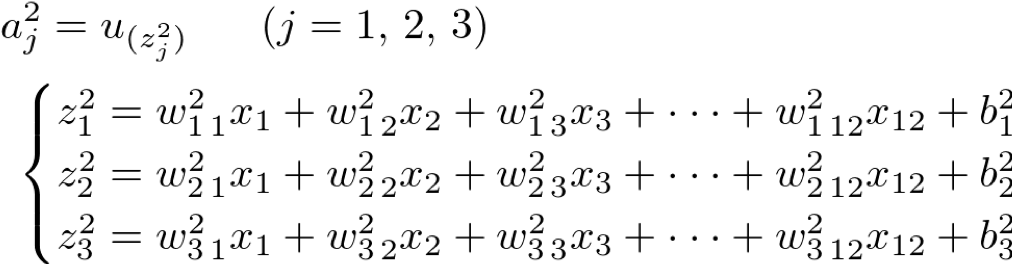
第3層:出力層(Output Layer)
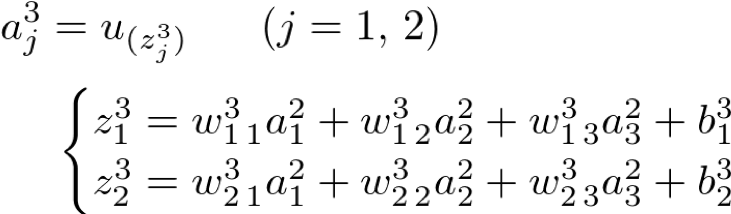
最後に
お疲れ様です!
これで、「ディープラーニングがどのようなモノか」が理解いただけたら嬉しいです。
でも、お気づきの方もいるとは思いますが、、、
「ディープラーニングの図解や数式は分かったけど、結局 パラメータってどうやって決めるの??」
と思われたでしょう。
そうです!
実は、まだディープラーニングというモノの説明しかしておらず、使い方の説明はできていません・・・
もし、ご自身でディープラーニングモデルをプログラミングするときは、パラメータを計算する優秀なパッケージが多数あります。
そのため、知らなくても何とかはなります。
ただ、気になる方、どうしても知りたい方へ向けて、次回は「パラメータの計算方法」を紹介します。
ある程度の高等数学の知識があることが前提の説明になってしまいますが、ご期待いただければと思います。





コメント